Improve Instrument Amplifier Performance with EMI Optimized Input Filter

Wm. P. (Bill) Klein, PE
Senior Technical Staff
Johanson Dielectrics, Inc
Feb. 19, 2009
ABSTRACT:
The common-mode rejection ability of an instrumentation amplifier degrades with increasing frequency often resulting in a major portion of the "advertised" bandwidth becoming unusable due to common-mode noise errors. An optimally designed passive input stage filter can provide significant improvement in AC common-mode rejection. Calculation of correct component values and selection of appropriate capacitors holds the key to the solution. A spreadsheet that gives graphic demonstration of the analysis and performs the necessary calculations to achieve this improvement is also included.
INSTRUMENTATION AMPLIFIERS & CMRR ERRORS
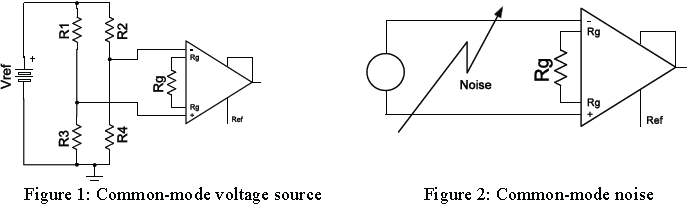
Instrumentation amplifiers are a very important element in analog signal processing. They provide one and only one service which is subtracting one voltage from another. Any signal that is common to both inputs (i.e.: common-mode voltage) must be rejected. Any common-mode voltage that is not rejected is converted to signal and therefore becomes an error at the output. This common-mode rejection error can introduce DC offset errors as well. The common-mode voltage may come from a common sensor bias circuit as shown in Figure 1, or as noise pick-up on long lines from the signal source to the instrumentation amplifier input pins as shown in Figure 2.
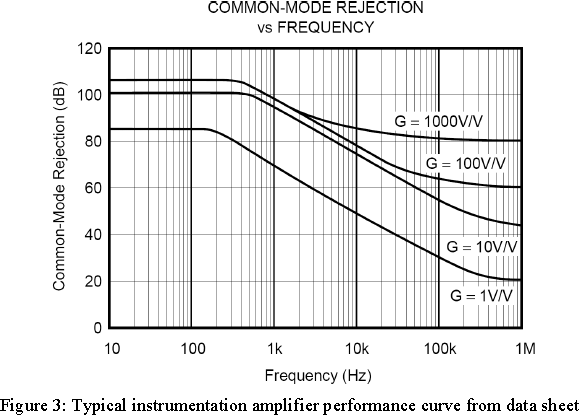
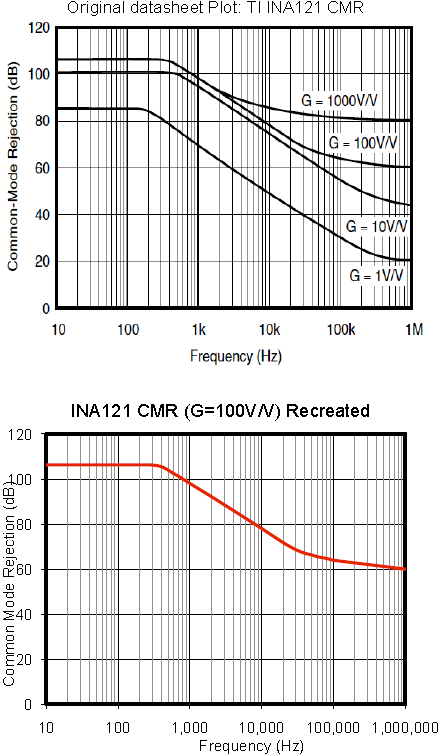
The ability of the instrumentation amplifier to eliminate the errors caused by this voltage is given by the Common-Mode Rejection Ratio (CMRR). In the specification tables this value describes performance at a very low frequency or DC and has minimum value in many applications. The CMRR performance at higher frequency is usually described by "Typical Performance" curves within the data sheet. Consider the plot in Figure 3. At a gain of 100V/V the CMRR is seen to decrease from about 105dB at a frequency of 400Hz. As the frequency increases from this point the CMRR drops at a rate of 20dB per frequency decade.
INPUT FILTER CONSIDERATIONS
Passive one-pole RC filters are commonly used ahead of each instrumentation amplifier input, as shown in Figure 4.
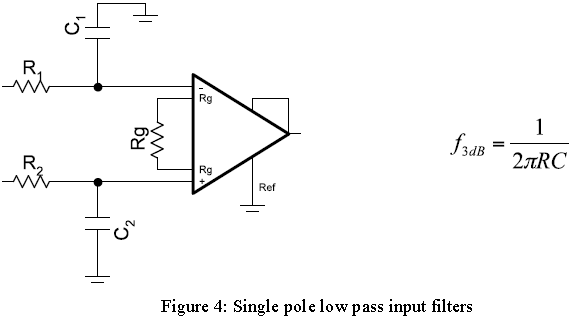
Conventional wisdom and published recommendations may suggest setting the low-pass filter's corner frequency at or near the amplifiers bandwidth, in this case 50 kHz (G=100.) Setting C1 = C2 = 1.0nF and R1 = R2 = 3.18kΩ establishes a pole frequency of 50 kHz.
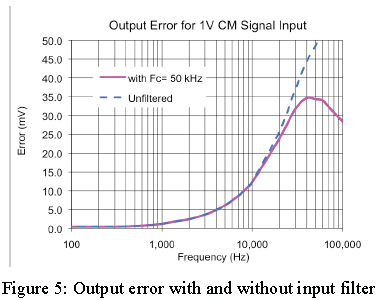
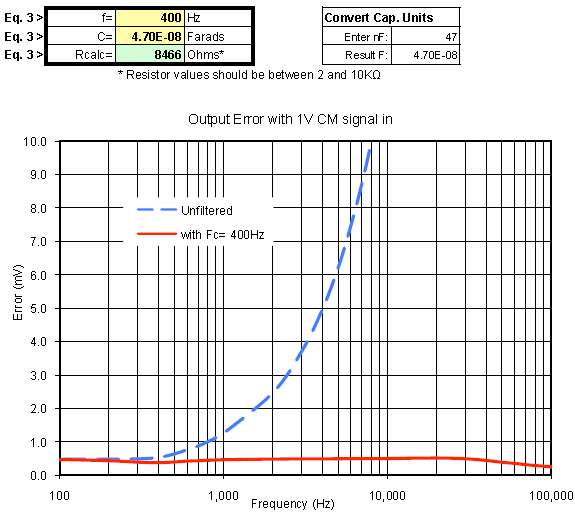
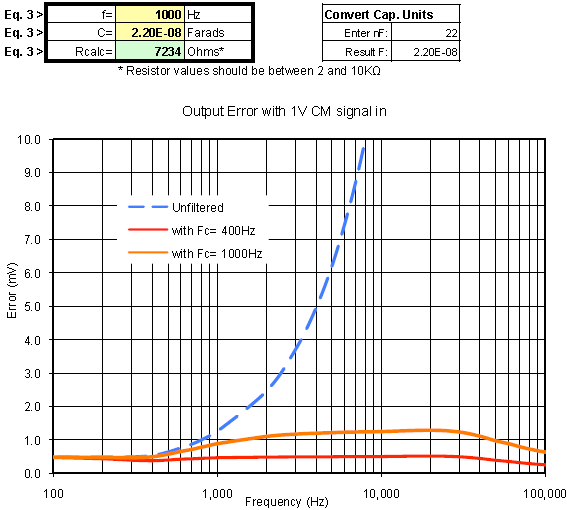
In figure 5 the output error voltage for a common-mode input of 1V is plotted for the unfiltered amplifier and with the 50kHz input stage filter. The amplifier gain of 100V/V is included in these calculations. Note that there is little improvement of system CMR due to the 50kHz filter until about 30kHz and signal error ranges between 1 and 35 mV/V from 1kHz to 40kHz. In many applications these error levels may be undesirable.
A CMR OPTIMIZED INPUT FILTER
Let's examine the error when the input filter pole frequency matches the frequency at which the given instrumentation amplifier's CMRR begins to degrade, in this case 400Hz. Setting C1 = C2 = 47.0nF and R1 = R2 = 8.5 kΩ establishes a 400Hz pole frequency. Figures 6 and 7 show two different scale views comparing this filters error signal with the previously discussed examples.
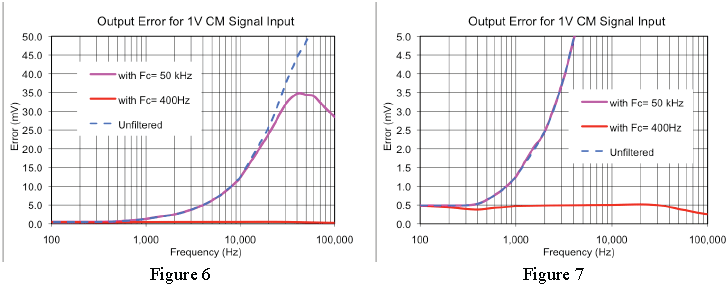
Adding the CMR optimized input stage filter has increased the effective common-mode rejection range by over two frequency decades limiting the CM error signal to just 0.5 mV. The trade-off is a reduction in system bandwidth. If additional bandwidth is required, setting the input filter pole frequency to 1kHz would limit CMR noise to 1.5mV and a 4kHz filter would hold CMR noise to 5mV.
IMPORTANCE OF FILTER MATCHING
The CMR analysis above assumed that the time constants between the positive and negative amplifier inputs are perfectly matched, that is R1C1 = R2C2. Notice that R1 and R2 are composed of the fixed resistors added to the sensor output impedance or the output impedance of the circuit driving this stage. Any imbalance in time constant between the two input filters will cause a difference signal to appear at the instrumentation amplifier inputs. This difference in voltage will be amplified and passed on to the next stage in the signal chain as if it were true signal which will be an error.
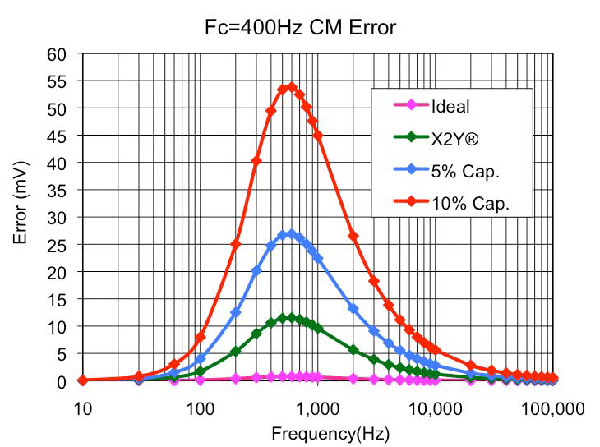
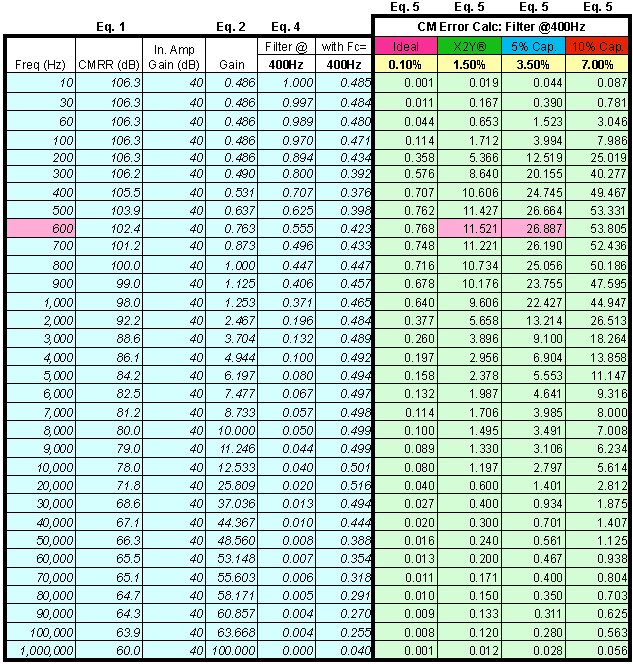
Figure 6 shows the magnitude of the expected error signal at the instrumentation amplifier output for various component mismatches with a 1Volt common-mode signal based on the 400Hz input filter RC values. Since the frequency response of each filter depends on that RC product, the instrumentation amplifier output error is determined by the sum of the of the component differences between the two sides. Resistors are widely available with a 0.1% tolerance at reasonable cost but tight tolerance capacitors have limited availability and can be expensive.
EMI MATCHED CAPACITOR CIRCUIT
The EMI capacitor is a possible solution due to the unique construction as shown in Figure 7. This device, with the internal reference element, provides a pair of matched, low inductance capacitors in a single component.
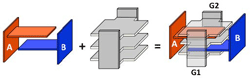
The result of this EMI construction is a capacitor pair where both halves are matched, voltage and temperature bias is equalized and aging effects on the dielectric are equal. This construction also requires a new graphic symbol for schematic drawing.
For conventional ceramic capacitors with ±10% or ±5% tolerance, a typical 1? distribution will yield a ±7.0% or ±3.5% variation in pair matching, respectively. The error curve for this level of mismatch is shown by the red and blue lines in Figure 6. The typical 1? distribution for the EMI capacitors from Johanson Dielectrics Inc. due to the construction topology is ±1.5%. This smaller mismatch yields the error curve shown as the green line in Figure 6. Additional matching benefits also result due to lower component mounting parasitics of the single EMI component vs. two discrete capacitors.
DIFFERENTIAL (X) CAPACITOR CONSIDERATIONS
For some high precision applications the small error introduced by even the EMI filter mismatch may still not be acceptable. It is possible to suppress the error caused by this mismatch with the addition of a differential filter capacitor labeled Cx in Figure 8.
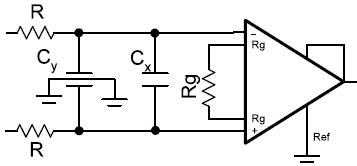
The value of Cx is determined by the frequency of the peak error and the attenuation required to reduce this error to an acceptable level. From the data plotted for Figure 6, the frequency of maximum error is 600Hz. At 600Hz the error is 11.5mV/V of common-mode signal for the ±1.5% curve and 26.9mV/V of common-mode signal for the ±3.5% curve. Determine the attenuation (A) required to meet system accuracy requirements at the frequency of peak error.
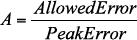
For calculations involving Cx any mismatch in the CMR filter components will not have a significant impact. Therefore:
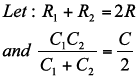
The required value of Cx to accomplish the needed error attenuation is given by:
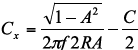
For the example, a 156nF Cx is required to contain the error for the ±1.5% mismatch case to 1mV, while a 387nF Cx is required to reduce the ±3.5% case to 1mV.
Cx improves common-mode rejection, but penalizes signal bandwidth. The frequency response for the Cx compensated filter can be calculated by:
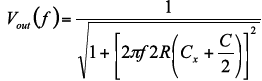
This is the signal chain frequency response and will appear as a single pole filter. The -3dB frequency is given by:
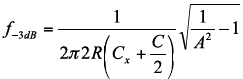
The resulting -3dB bandwidth is 52.3Hz and 22.9Hz for the two examples.
The results of these calculations show that the improved match inherent in the EMI capacitor design provides more than twice the signal bandwidth of the conventional ceramic capacitors for the same CMRR performance. All of this is accomplished without the cost of selecting matched capacitors.
SUMMARY
Input amplifier errors result when common-mode Signals are present on the amplifier inputs. The Common-Mode Rejection Ratio (CMRR) of Input Amplifiers can be improved at higher frequencies by employing properly designed input filters featuring balanced time-constants. Some applications may require an X capacitor across the amplifier input to negate input filter imbalances. Instrumentation amplifier bandwidth is sacrificed when employing these CM noise reduction techniques. In many applications, a single EMI capacitor can effectively replace two tight tolerance Y capacitors plus the X capacitor. A spreadsheet is available containing the calculators and simulation graphs used in this paper and it's Appendix.
ABOUT THE AUTHOR
William P. (Bill) Klein has over 40 years experience as an analog circuit designer in fields ranging from mineral exploration to medical nuclear imaging. Bill joins Johanson Dielectrics, Inc. technical staff after a 15 year position as Senior Applications Engineer for Texas Instruments Precision Analog Group; authoring numerous magazine articles, application notes, conference papers; and hosting TI's Analog e-LAB Webcast series.
APPENDIX 1: CALCULATION PROCEDURES
A spreadsheet program was developed to calculate the system response of an instrumentation amplifier/input-filter combination to common-mode signals over a frequency band. This Appendix details the calculation steps so that they might be applied to other amplifier and filter scenarios.
The first task is to capture the amplifier CMR vs. Frequency data. Enlarge the curve from the data sheet to a full-page size and print it out for easier measurement. Larger size allows more accurate curve measurement.
For the example in this paper a ratio technique was used to find the values to enter in the spreadsheet. Consider the following example of enlarged CMR plot of a TI INA121.
The distance between the grid lines measured 25.5mm.
The grid lines are at 20dB increments.
At 1kHz the 100V/V line is 23 mm above the 80dB grid.
Therefore the CMR at 1kHz is:
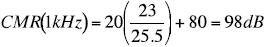
The curve being copied generally gives CMR as a positive number so the actual signal gain of the instrumentation amplifier, in dB, must be subtracted from it. This calculation gives the common-mode signal gain through the amplifier as a function of frequency.
Convert this value from db to Volts/Volt at each frequency with the following relationship.
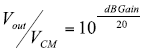
A plot of this value will give the curve shown in Figure: 5 with the No Filter label.
Estimate the frequency where the CMR vs. Frequency curve parts from the DC value. This will be a good starting frequency for the corner frequency for the design of the filter. As given in the paper, select the R and C values to satisfy the expression:
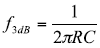
Calculate the filter frequency response from the following equation:
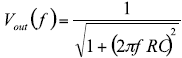
Multiply this value times the V/V in Eq. 2 to obtain the total system gain. A plot of these values gives the second curve in Figure 5. It may require some trial and error to find the best value for the corner frequency.
To calculate the error due to component mismatch set a column in the spreadsheet to compute:
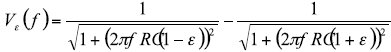
The results of this calculation are presented in Figure 6.
From the data plotted for Figure 6 the frequency of maximum error is 600Hz. At 600Hz the error is 11.5mV/V of common-mode signal for the ±1.5% curve and 26.9mV/V of common-mode signal for the ±3.5% curve. Determine the attenuation (A) required to meet system accuracy requirements at the frequency of peak error.
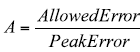
For calculations involving Cx any mismatch in the CMR components will not have a significant impact. Therefore:
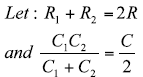
The required value of Cx to accomplish the needed error attenuation is given by:
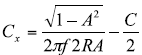
For the example the capacitor values are 156nF for the lesser error and 387nF for the greater error to reduce the error to 1mV. The frequency response for the Cx compensated filter can be calculated by:
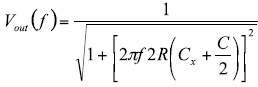
This is the signal chain frequency response and will appear as a single pole filter. The -3dB frequency is given by:
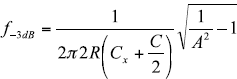
The resulting -3dB bandwidth is 52.2Hz and 22.3Hz for the two examples.
Graphic to Numeric Conversion of CMR Data
This worksheet converts graphical CMR data into numerical CMR data for further simulation. Physical measurements taken from an enlarged datasheet plot for a TI INA121 are entered in the yellow cells and dB data is returned in the green cells based on the mm/db ratio of the plot (see Eq. 2 of Appendix.) Numerical data is replotted in red for a visual confirmation.
| Measurement Ratio Data | ||
|---|---|---|
| dB/div | mm/div | dB/mm |
| 20 | 25.5 | 0.78431 |
| Freq. (Hz) | Baseline (dB) | Offset (mm) | CMRR (dB) |
|---|---|---|---|
| 10 | 100 | 8 | 106.3 |
| 30 | 100 | 8 | 106.3 |
| 60 | 100 | 8 | 106.3 |
| 100 | 100 | 8 | 106.3 |
| 200 | 100 | 8 | 106.3 |
| 300 | 100 | 7.9 | 106.2 |
| 400 | 100 | 7 | 105.5 |
| 500 | 100 | 5 | 103.9 |
| 600 | 100 | 3 | 102.4 |
| 700 | 100 | 1.5 | 101.2 |
| 800 | 100 | 0 | 100.0 |
| 900 | 80 | 24.2 | 99.0 |
| 1,000 | 80 | 23 | 98.0 |
| 2,000 | 80 | 15.5 | 92.2 |
| 3,000 | 80 | 11 | 88.6 |
| 4,000 | 80 | 7.8 | 86.1 |
| 5,000 | 80 | 5.3 | 84.2 |
| 6,000 | 80 | 3.22 | 82.5 |
| 7,000 | 80 | 1.5 | 81.2 |
| 8,000 | 80 | 0 | 80.0 |
| 9,000 | 80 | 24.2 | 79.0 |
| 10,000 | 60 | 23 | 78.0 |
| 20,000 | 60 | 15 | 71.8 |
| 30,000 | 60 | 11 | 68.6 |
| 40,000 | 60 | 9 | 67.1 |
| 50,000 | 60 | 8 | 66.3 |
| 60,000 | 60 | 7 | 65.5 |
| 70,000 | 60 | 6.5 | 65.1 |
| 80,000 | 60 | 6 | 64.7 |
| 90,000 | 60 | 5.5 | 64.3 |
| 100,000 | 60 | 5 | 63.9 |
| 1,000,000 | 60 | 0 | 60.0 |
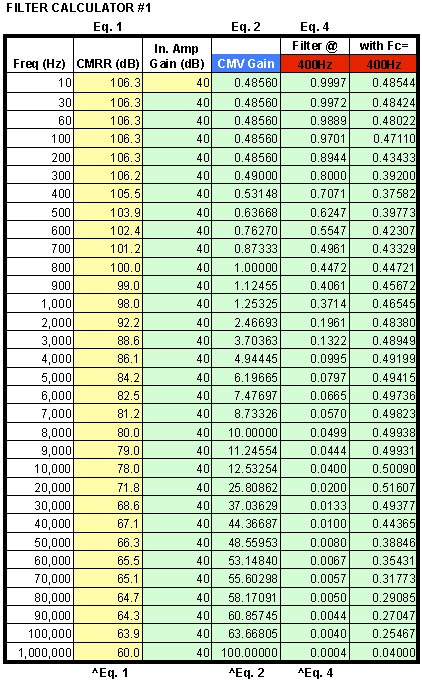
Filter Response Calculator
This worksheet calculates and plots Instrumentation Amplifier output results based on a 1V common mode input. Calculator#2 below plots an alternate filter design. Both unfiltered and filtered signals are plotted and the single pole input filter frequency may be changed. The CMRR and amplifier gain may be changed to reflect other devices.
Equations from the white paper are referenced.
Yellow cells may be changed, green cells are calculated results.
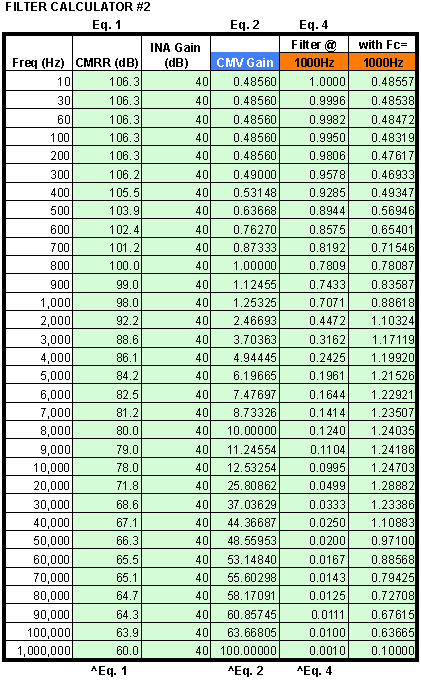
Filter Response Calculator
Use this calculator 2 to calculate and generate a comparison plot of other RC combinations with the CM optimized filter above.
Time Constant Error Plot & Xcap Calculator
This worksheet calculates and plots output error results due to unequal input filter time constants based on a 1V common mode input. The theoretical minimum value X capacitor (Cx) needed to attenuate this error is calculated based on Peak Error, Peak Error Frequency, and Desired Error entered from the red cells in the CM Error Calc table. Resulting system bandwidth is also calculated. (Blue cell values are imported from Filter Calculator #1. Yellow cells may be changed, green cells are calculated results.)